2018中考数学压轴题(43)

2018-04-09 14:58:26来源：网络

【课程】

新初一秋季课程

新初二秋季课程

新初三秋季课程

新高一秋季课程

【备考】语文资料英语资料数学资料物理资料化学复习资料政治资料历史复习资料地理资料

　　新东方在线中考网整理了《2018中考数学压轴题(43)》，供同学们和家长参考。

　　(1)求抛物线的解析式;

　　(2)如图2，当动点P只在第一象限的抛物线上运动时，求过点P作PF⊥BC于点F，试问△PDF的周长是否有最大值?如果有，请求出其最大值，如果没有，请说明理由.

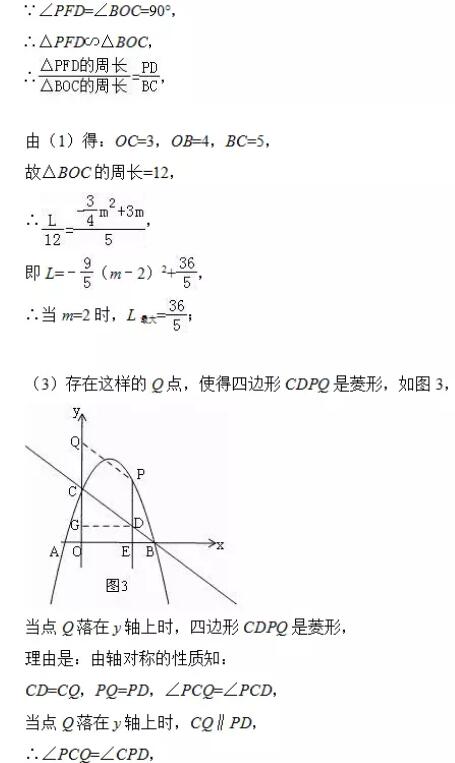
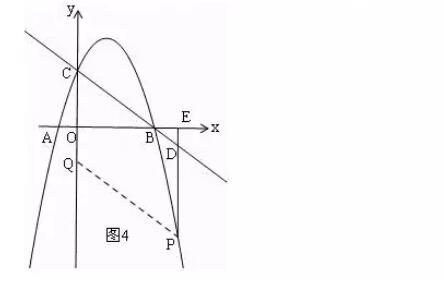
　　(3)当点P在抛物线上运动时，将△CPD沿直线CP翻折，点D的对应点为点Q，试问，四边形CDPQ是否成为菱形?如果能，请求出此时点P的坐标，如果不能，请说明理由.

2018中考数学压轴题(43)

　　考点分析：

　　二次函数综合题.

　　题干分析：

　　(1)利用待定系数法求二次函数的解析式;

　　(2)设P(m，﹣3/4 m2+9/4m+3)，△PFD的周长为L，再利用待定系数法求直线BC的解析式为：y=﹣3/4x+3，表示PD=﹣3/4m²+3m，证明△PFD∽△BOC，根据周长比等于对应边的比得：△PFD的周长/△BOC的周长=PD/BC，代入得：L=﹣9/5(m﹣2)2+36/5，求L的最大值即可;

　　(3)如图3，当点Q落在y轴上时，四边形CDPQ是菱形，根据翻折的性质知：CD=CQ，PQ=PD，∠PCQ=∠PCD，又知Q落在y轴上时，则CQ∥PD，由四边相等：CD=DP=PQ=QC，得四边形CDPQ是菱形，表示P(n，﹣3/4 n2+9/4n+3)，则D(n，﹣3/4 n+3)，G(0，﹣3/4 n+3)，利用勾股定理表示PD和CD的长并列式可得结论。

　　解题反思：

　　本题是二次函数的综合题，考查了利用待定系数法求函数的解析式、菱形的性质和判定、三角形相似的性质和判定，将周长的最值问题转化为二次函数的最值问题，此类问题要熟练掌握利用解析式表示线段的长，并利用相似比或勾股定理列方程解决问题。

　　更多中考资料下载、中考最新资讯、中考录取分数、中考体育等最新中考信息，请关注新东方在线中考网。

　　相关推荐：

　　2017中考真题试卷汇总

　　2017中考成绩查询及录取分数线

　　2017北京中考成绩查询及录取分数线

8科2018中考复习资料大全(下载版)
序号	2018中考复习资料大全	查看详情
1	2018中考语文复习资料大全(下载版)	点击查看
2	2018中考数学资料大全(下载版)	点击查看
3	2018中考英语复习资料大全(下载版)	点击查看
4	2018中考物理资料大全(下载版)	点击查看
5	2018中考化学复习资料大全(下载版)	点击查看
6	2018中考地理复习资料大全(下载版)	点击查看
7	2018中考历史复习资料大全(下载版)	点击查看
8	2018中考政治复习资料大全(下载版)	点击查看