新概念英语 英语提升 免费课 英语水平测试 一对一辅导

新东方在线 > 初中 > 初一 > 初一数学 > 正文

初一数学指导：一元一次方程不掌握这9种题型

2017-12-05 11:26:01来源：网络

　　题型一：数字问题

　　(1)多位数字的表示方法：

　　一个两位数的十位数字、个位数字分别为a、b，(其中a、b均为整数， 1≤a≤9，0≤b≤9)则这个两位数可以表示为10a+b

　　一个三位数的百位数字为a，十位数字为b，个位数字为c，(其中均为整数，且1≤a≤9，0≤b≤9，0≤c≤9)则这个三位数表示为：100a+b+c

　　(2)奇数与偶数的表示方法：偶数可表示为2k，奇数可表示为2k+1(其中k表示整数)

　　(3)三个相邻的整数的表示方法：可设中间一个整数为a，则这三个相邻的整数可表示为a-1,a,a+1

　　例1 一次数学测验中，小明认为自己可以得满分，不料卷子发下来一看得了96分，原来是由于粗心把一个题目的答案十位与个位数字写颠倒了，结果自己的答案比正确答案大了36，而正确答案的个位数字是十位数字的2倍.正确答案是多少?

　　例2 某年份的号码是一个四位数，它的千位数字是2，如果把2移到个位上去，那么所得的新四位数比原四位数的2倍少6，求这个年份。

　　题型二：日历问题

　　(1)在日历问题中，横行相邻两数相差1，竖列相邻两数相差7.

　　(2)日历中一个竖列上相邻3个数的和的最小值时24，最大值时72，且这个和一定是3的倍数.

　　(3)一年中，每月的天数是有规律的，一、三、五、七、八、十、十二这七个月每月都是31天，四、六、九、十一这四个月每月都是30天，二月平年28天，闰年29天，所以，日历表中日期的取值是有范围的.

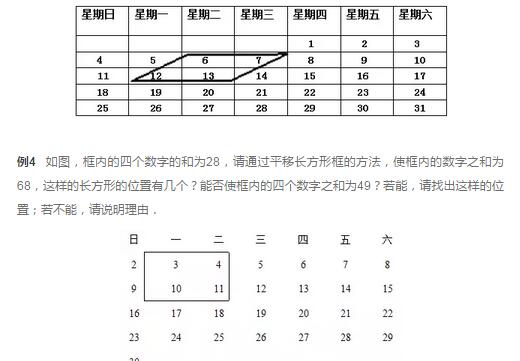
　　例3 下表是2011年12月的日历表，请解答问题：在表中用形如下图的平行四边形框框出4个数，

　　(1)若框出的4个数的和为74，请你通过列方程的办法，求出它分别是哪4天?

　　(2)框出的4个数的和可能是26吗?为什么?

　　题型三：和差倍分问题

　　和、差、倍问题关键要分清是几倍多几和几倍少几.

　　(1)当较大量是较小量的几倍多几时，;

　　(2)当较大量是较小量的几倍少几时，.

　　例5 一部拖拉机耕一片地，第一天耕了这片地的;第二天耕了剩下部分的，还剩下42公顷没耕完，则这片地共有多少公顷?

　　例6 牧羊人赶着一群羊寻找一个草长得茂盛的地方，一个过路人牵着一只肥羊从后面跟了上来，他对牧羊人说：“你赶的这群羊大概有100只吧!”牧羊人答道：“如果这群羊增加一倍，再加上原来这群羊的一半，又加上原来这群羊一半的一半，连你这只羊也算进去，才刚好凑满100只.”问牧羊人的这群羊共有多少只?

　　题型四：行程问题

　　1.行程问题

　　路程=速度×时间

　　相遇路程=速度和×相遇时间

　　追及路程=速度差×追及时间

　　2.流水行船问题

　　顺流速度=静水速度+水流速度

　　逆流速度=静水速度-水流速度

　　水流速度=×(顺流速度-逆流速度)

　　3.火车过桥问题

　　火车过桥问题是一种特殊的行程问题，需要注意从车头至桥起，到车尾离桥止，火车所行距离等于桥长加上车长，列车过桥问题的基本数量关系为：

　　车速×过桥时间=车长+桥长.

　　例7 有甲、乙、丙三人同时同地出发，绕一个花圃行走，乙、丙二人同方向行走，甲与乙、丙背向而行.甲每分钟走40米，乙每分钟走38米，丙每分钟走36米.出发后，甲和乙相遇后3分钟和丙相遇，求花圃的周长.

　　例8 某人从家里骑摩托车到火车站，如果每小时行30千米，那么比火车开车时间早到15分钟，若每小时行18千米，则比火车开车时间迟到15分钟，现在此人打算在火车开车前10分钟到达火车站，则此人此时骑摩托车的速度应为多少?

　　例9 一小船由A港到B港顺流需行6小时，由B港到A港逆流需行8小时，一天，小船从早晨6点由A港出发顺流行至B港时，发现一救生圈在途中掉落在水中，立即返回，1小时后找到救生圈.问：

　　(1)若小船按水流速度由A港漂流到B港需多少小时?

　　(2)救生圈是何时掉入水中的?

　　题型五：工程问题

　　工作总量=工作时间×工作效率

　　各部分工作量之和=1

　　例10 有甲、乙、丙三个水管，独开甲管5小时可以注满一池水;甲、乙两管齐开，2小时可注满一池水;甲、丙两管齐开，3小时注满一池水.现把三管一齐开，过了一段时间后甲管因故障停开，停开后2小时水池注满.问三管齐开了多少小时?

　　例11 检修一住宅区的自来水管道，甲单独完成需14天，乙单独完成需18天，丙单独完成需12天.前7天由甲、乙两人合作，但乙中途离开了一段时间，后2天由乙、丙两人合作完成，问乙中途离开了几天?

　　题型六：商品销售问题

　　在现实生活中，购买商品和销售商品时，经常会遇到进价、标价、售价、打折等概念，在了解这些基本概念的基础上，还必须掌握以下几个等量关系：

　　利润=售价-进价

　　利润=进价×利润率

　　实际售价=标价×打折率

　　例12 某商场经销一种商品，由于进货时价格比原进价降低了，使得利润增加了8个百分点，求经销这种商品原来的利润率。

　　例13 某商品月末的进货价为比月初的进货价降了8%，而销售价不变，这样，利润率月末比月初高10%，问月初的利润率是多少?

　　题型七：方案决策问题

　　在实际生活中，做一件事情往往会有多种选择，这就需要从几种方案中，选择最佳方案，如网络的使用，到不同旅行社购票等，一般都要运用方程解答，把每一种方案的结果先算出来，进行比较后得出最佳方案。

　　例14 某开发商进行商铺促销，广告上写着如下条款：

　　投资者购买商铺后，必须由开发商代为租赁5年，5年期满后由开发商以比原商铺标价高20%的价格进行回购，投资者可在以下两种购铺方案中做出选择：

　　方案一：投资者按商铺标价一次性付清铺款，每年可以获得的租金为商铺标价的10%.

本文关键字: 初一数学　一元一次方程

上一页 1 2 3 下一页

微信扫码加入【初中群】免费领取

6G初中全科学习资料

更多资料

微信扫码加入【初中福利群】

6G初中全科学习资料

  • 1.手机微信【扫一扫】识别上方二维码
  • 2.加入【初中福利群】免费领取初中学习资料
更多>>
更多内容

初中学英语资料大礼包合集

扫描下方二维码自动领取

初中资料
更多>>
更多英语课程>>
  • 1
  • 2
  • 3
  • 4
  • 5
  • 6
  • 7
  • 8
  • 9
  • 10